AdaBoost
1. Boosting
Problems in machine learning often consist of a large number of features. This can cause difficulties in training and generalization properties. Boosting is a type of algorithm that focuses on the most relevant features iteratively, selecting only those features that improve the model.
Consider a binary classification model with labels \(\{-1,1\}\). In adaboost or adaptive boosting, we fit a series of weak-learners iteratively. A weak-learner is an algorithm that performs only slightly better than chance. An example can be a decision tree with small depth. At each step in adaboosting, a new weak learner is fitted to the data but using different weights so that the algorithm focus on the datapoints it finds harder to classify.
After the mth-step the classifier will have the form
\[C_{m}(x)=\alpha_1h_1(x)+\ldots+\alpha_{m}h_{m}(x)\]In each step we minimize the exponential loss function by choosing $\alpha$. At the mth step this loss function is
\[\frac{1}{N}\sum_{i=1}^N e^{-y_i C_m(x_i)}=\frac{1}{N}\sum_{i=1}^N e^{-y_i C_{m-1}(x_i)-y_ih_m(x_i)\alpha_m}=\sum_i \omega_i e^{-y_ih_m(x_i)\alpha_m}\]where $\omega_i=e^{-y_iC_{m-1}(x_i)}/N$ is a weight, and we fit the mth weak learner $h_m(x)$ on the data weighted by $\omega_i$. Differentiating with respect to $\alpha_m$ and setting to zero we obtain
\[\begin{equation*}\begin{split}&\sum_i\omega_i y_ih_m(x_i)e^{-y_ih_m(x_i)\alpha_m}=0\iff \\ &\sum_{y_i=h_m(x_i)}\omega_ie^{-\alpha_m}-\sum_{y_i\neq h_m(x_i)}\omega_ie^{\alpha_m}=0\iff \frac{\sum_{y_i=h_m(x_i)}\omega_i}{\sum_{y_i\neq h_m(x_i)}\omega_i}=e^{2\alpha_m}\end{split}\end{equation*}\]Normalizing the weights such that $\sum_i\omega_i=1$, we calculate the parameter $\alpha_m$ as
\[\alpha_m=\frac{1}{2}\ln\Big(\frac{1-\sum_{y_i\neq h_m(x_i)}\omega_i}{\sum_{y_i\neq h_m(x_i)}\omega_i}\Big)=\frac{1}{2}\ln\Big(\frac{1-\epsilon_m}{\epsilon_m}\Big)\]where $\epsilon_m$ is the weighted error
\[\epsilon_m=\sum_{y_i\neq h_m(x_i)}\omega_i\]For $m=1$, the first step, the weights are $\omega_i=1/N$.
In summary the algorithm consists:
w=1/N # weight initialization
learners=[] # list of weak learners
for i in range(T):
Weak_Learner.fit(x_train,y_train,weights=w)
error=Weak_Learner.score(x_train,y_train,weights=w)
alpha=0.5 log(1-error/error)
learners.append(alpha*Weak_Learner)
w=Weight.recalculate(w)
#predictor function
def C(x):
prediction=0
for wl in learners:
prediction+=wl.predict(x)
return sign(prediction)
2. Decision Boundary
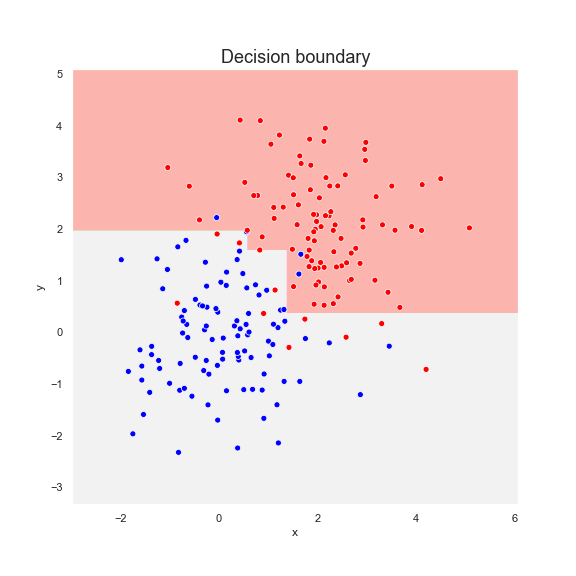
We fit an Adaboost classifier to a dataset consisting of two sets of points, red and blue, normally distributed. Below is the Adaboost prediction after six steps.
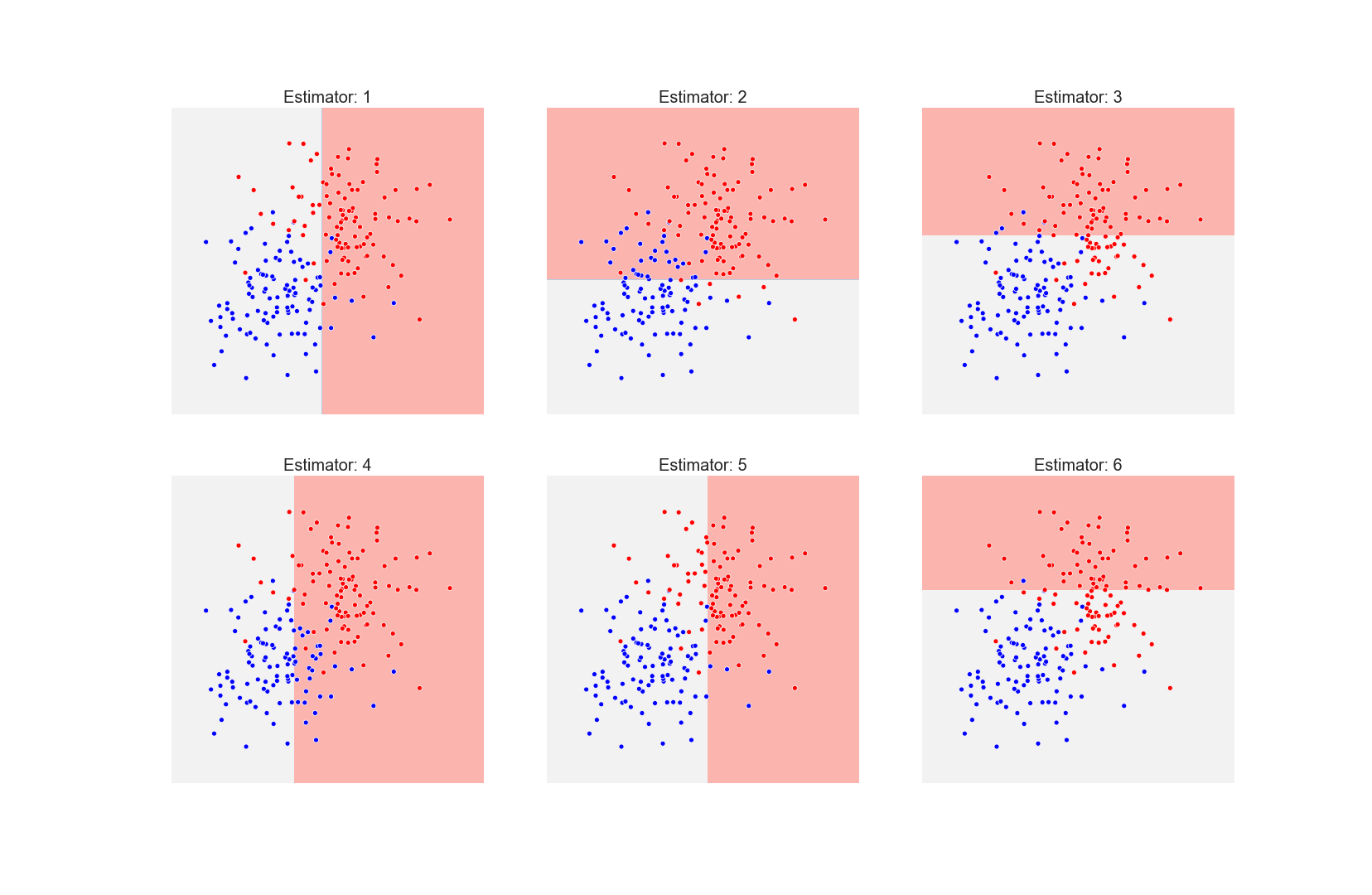
And below we present the prediction of its six estimators in the order of training, from left to right
At each step we superimpose the prediction from the previous estimatores:
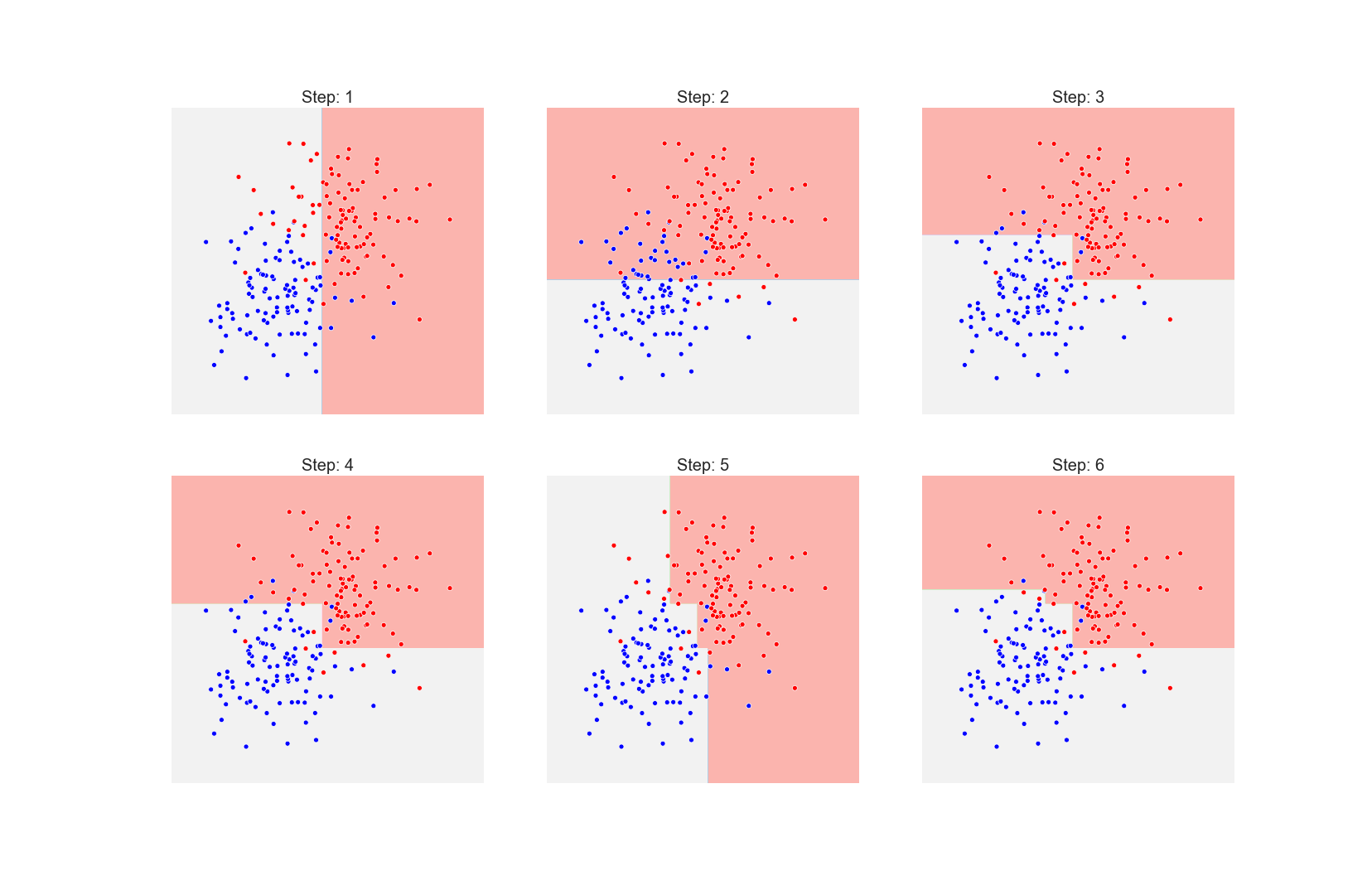
One can see that at each step the alogrithm tries to “fix” the misclassified points.
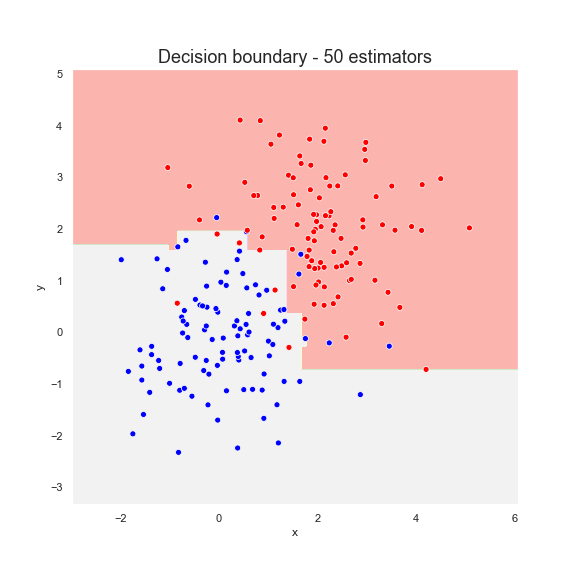
With more estimators, the decision boundary becomes more complex
3. Python Implementation
We build a class node that stores the weak learners. The attribute “next” points to the next weak-learner in the series.
class node:
def __init__(self,alpha=None,tree=None):
self.tree=tree
self.alpha=alpha
self.next=None
def insert(self,alpha,tree):
if self.next is None:
self.next=node(alpha,tree)
else:
return self.next.insert(alpha,tree)
The class Adaboost contains fit and predict methods.
class AdaBoost:
def __init__(self,T):
self.T=T
self.head=node(alpha=1,tree=DecisionTreeClassifier(max_depth=1))
def step(self,ypred,y,sample_weight):
error=1-accuracy_score(y,ypred,sample_weight=sample_weight)
if error==1.0:
return 'stop'
else:
alpha=0.5*np.log((1-error)/error)
sample_weight=sample_weight*np.exp(-y*ypred*alpha)
sample_weight=sample_weight/sample_weight.sum()
return alpha, sample_weight
def fit(self,x,y):
sample_weight=np.ones(x.shape[0])
self.head.tree.fit(x,y)
ypred=self.head.tree.predict(x)
alpha, sample_weight=self.step(ypred,y,sample_weight)
self.head.alpha=alpha
for i in range(1,self.T):
tree=DecisionTreeClassifier(max_depth=1)
tree.fit(x,y,sample_weight=sample_weight)
ypred=tree.predict(x)
alpha, sample_weight=self.step(ypred,y,sample_weight)
self.head.insert(alpha,tree)
def read(self,node,x):
ypred=node.tree.predict(x)
ypred=node.alpha*ypred
if node.next is None:
return ypred
else:
return ypred+self.read(node.next,x)
def predict(self,x):
ypred=self.read(self.head,x)
ypred=np.sign(ypred)
return ypred