Convolutional Neural Network
1. Convolutional neural network
A convolutional neural network incorporates geometrical features in the learning algorithm. The neural network uses the convolution operation to capture the spatial correlation between data at different positions. This type of architecture is most suitable for vision tasks like image classification. The convolution amounts to a linear operation over smaller regions of the image, much like a moving average, except that this is not normalized. More explicitly, for a matrix of pixels $m_{ij}$ with size $N\times N$, and a kernel $K$ with weights $w_{\mu\nu}$ and size $k\times k$ we calculate
\[K(m_{ij})=\sum_{\mu,\nu=0}^{k-1} w_{\mu\nu}m_{i+\mu,j+\nu}+b\]where $b$ is a bias. The convolution operation is depicted in the picture below for a kernel of size $4\times4$.

The convolution runs over the pixels where the kernel is allowed to be inside the image. That is, we have $m_{i+\mu,j+\nu}=m_{i’j’}$. We can relax this condition and allow for a padding $P$ that we add at the beginning and end of the image. Then we ensure that all pixels living in the padding regions are zero, that is, $m_{ij}=0$ for $i,j\in [-P,0[\,\cup\, ]N-1,N-1+P]$. One can also define a stride $S$ that determines the pixels the kernel runs over, that is, $(i,j)=(-P\text{ mod}(S),-P \text{ mod(S)})$. Therefore, if the pixel matrix has size $N\times N$ then the output of the convolution has shape $N’\times N’$ with
\[N'=(N+2P-k+1)//S+1\]After the convolution operation, we apply a non-linear activation function on each element of the matrix \(m'_{i'j'}\). The result is the output of a convolutional layer. Besides, one can create channels whereby we apply multiple kernels to the same input. So if the kernel \(K^c\) has C channels, the convolutional layer’s output is $C$ matrices \(m^c_{i'j'}\). Similarly, for each matrix \(m^c_{i'j'}\) one can further apply a kernel with \(C'\) channels. The result of using first the kernel \(K^c\), and then \(K^{c'}\) is \(C\times C'\) matrices.
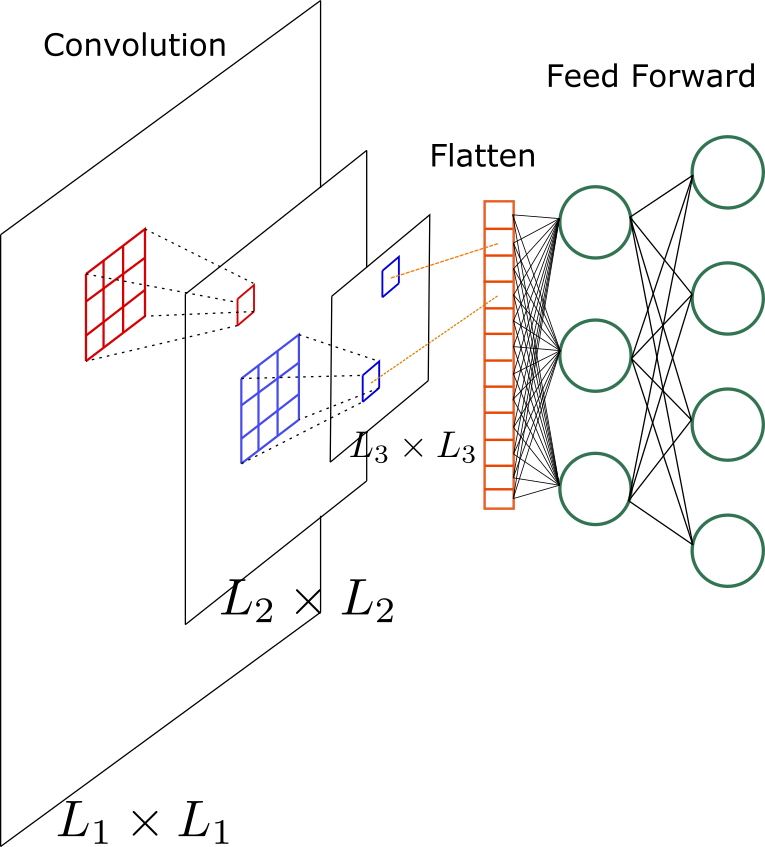
After the convolutional layers, the resulting matrix is flattened and added as an input to a feed-forward neural network. Below we show this series of operations.
2. Python implementation
Using the grad_lib library that we have built in the previous post, we can build neural networks more easily. First we define a convolutional neural network
Convolutional Neural Network (1 channel)
from grad_lib import Tensor, ReLU, FeedForward, Softmax, LinearLayer, Log, DataSet
class ConvNet2D:
def __init__(self,kernel_size,img_size=(8,8),stride=1,padding=0):
"""Convolutional Layer with 2D kernel
Args:
kernel_size ([type]): [description]
img_size (tuple, optional): [description]. Defaults to (8,8).
stride (int, optional): [description]. Defaults to 1.
padding (int, optional): [description]. Defaults to 0.
"""
self.img_size=img_size
self.stride=stride
self.pad=padding
self.kernel_shape=(kernel_size,kernel_size)
weight, bias=self.init_param()
self.kernel=Tensor(weight.reshape(1,-1),requires_grad=True)
self.bias=Tensor(bias,requires_grad=True)
self.out_dim=self.get_out_dim()
self.relu=ReLU()
"""trainable Tensors
"""
self.trainable={id(self.kernel): self.kernel,
id(self.bias): self.bias
}
def __call__(self,x):
"""forward
Args:
x (Tensor): (batch,S,S)
Returns:
Tensor: (batch,num_neurons)
"""
x_tensor=self.transform(x.array)
out=self.kernel*x_tensor+self.bias
out=self.relu(out)
return out.squeeze(0)
def init_param(self):
weight=np.random.normal(0,1,self.kernel_shape)
bias=np.random.normal(0,1,(1,1))
return weight, bias
def transform(self,x):
"""transform batch of images
Args:
x (numpy.array): (batch,S,S)
Returns:
Tensor: (kernel_size**2,batch,num_neurons)
"""
# x: array
i_f=x.shape[1]+self.pad-self.kernel_shape[0]
j_f=x.shape[2]+self.pad-self.kernel_shape[1]
out_list=[]
for k in range(x.shape[0]):
out=np.zeros((1,self.kernel_shape[0]*self.kernel_shape[1]))
for i in range(0,i_f+1,self.stride):
for j in range(0,j_f+1,self.stride):
z=x[k,i:i+self.kernel_shape[0],j:j+self.kernel_shape[1]].reshape(1,-1)
out=np.concatenate([out,z],axis=0)
out_list.append(out[1:])
#out_list: [batch,num_neurons,kernel_size**2]
out=np.array(out_list).transpose(2,0,1)
return Tensor(out,requires_grad=False)
def get_out_dim(self):
test=np.zeros((1,self.img_size[0],self.img_size[1]))
size=self.transform(test).shape
return size[2]
Convolutional neural network model for multi-class problem
class ConvClassifier:
def __init__(self,img_size,hidden_dim,out_dim=1):
"""Convolutional Neural Network Classifier
Args:
img_size (tuple): (width,height)
hidden_dim (int): number of hidden neurons
out_dim (int, optional): number of class. Defaults to 1.
"""
self.convnet=ConvNet2D(kernel_size=3,img_size=img_size)
in_dim=self.convnet.out_dim
self.in_layer=LinearLayer(in_dim,hidden_dim)
self.out_layer=LinearLayer(hidden_dim,out_dim)
self.softmax=Softmax()
self.relu=ReLU()
def __call__(self,x):
"""[summary]
Args:
x (numpy.array): input must be array, not Tensor
Returns:
probability: (batch,out_dim)
"""
out=self.convnet(x)
out=self.in_layer(out)
out=self.relu(out)
out=self.out_layer(out)
prob=self.softmax(out)
return prob
@staticmethod
def train():
Tensor.calc_grad=True
@staticmethod
def eval():
Tensor.calc_grad=False
Cross-Entropy loss and Optimizer
We also need to write the cross-entropy loss function and optimizer.
class CrossEntropyLoss:
def __init__(self,model):
self.model=model
self.log=Log()
def __call__(self,prob,y):
"""loss function
Args:
prob (probability Tensor): (batch,num_classes)
y (array): (batch,1)
"""
bsz=y.shape[0]
prob_=prob[range(bsz),y[:,0]]
loss=-self.log(prob_).sum(0)
loss=(1/bsz)*loss
self.back_grads=loss.grad
return loss.array
def backward(self):
self.model.grads=self.back_grads
class Optimizer:
def __init__(self,model,lr):
self.model=model
self.lr=lr
self.tensors={}
for _,obj in self.model.__dict__.items():
if hasattr(obj,'trainable'):
self.tensors.update(obj.trainable)
def zero_grad(self):
for idx, tensor in self.tensors.items():
if tensor.requires_grad:
grad={}
grad[idx]=tensor.grad[idx]
tensor.grad=grad
else:
grad={'none':0}
tensor.grad=grad
def step(self):
if self.model.grads is not None:
for idx, tensor in self.tensors.items():
if idx in self.model.grads:
tensor.array-=self.lr*self.model.grads[idx]
else:
print('No grads!')
Training function
def train(model,loss,optimizer,data_loader,epochs):
model.train()
L=len(data_loader)
for epoch in tqdm(range(epochs)):
total_loss=0
for batch in data_loader:
batch_x,batch_y=batch
bsz=batch_x.shape[0]
optimizer.zero_grad()
pred=model(batch_x)
total_loss+=loss(pred,batch_y.array)*bsz
loss.backward()
opt.step()
print('Epoch: ',epoch," Loss: ",total_loss/L)
Example
Use the $8\times8$ version of the MNIST dataset as a toy-model.
from sklearn.datasets import load_digits
data=load_digits()
imgs=data['data']
target=data['target']
#normalize the pixels for easier training
img_norm=imgs/16
#create iterator
data_loader=DataSet(img_norm,target,batch_size=64)
model=ConvClassifier(img_size=(8,8),hidden_dim=10,out_dim=10)
loss=CrossEntropyLoss(model)
opt=Optimizer(model,lr=0.1)
train(model,loss,opt,data_loader,10)