Clustering K-Means
Kmeans algorithm
Kmeans clustering is an unsupervised machine learning algorithm. Given a set of data-points and the number of clusters the algorithm assigns each point to a particular cluster. The algorithm works iteratively starting from N randomly assigned cluster positions, and subsequently changing the positions until convergence is achieved.
The algorithm follows the steps:
- Choose random positions for the clusters;
- For each data-point determine the closest cluster;
- Calculate the center-of-mass for each group, which is now the new cluster center position;
- Loop through 2,3 until a certain degree of convergence is achieved.
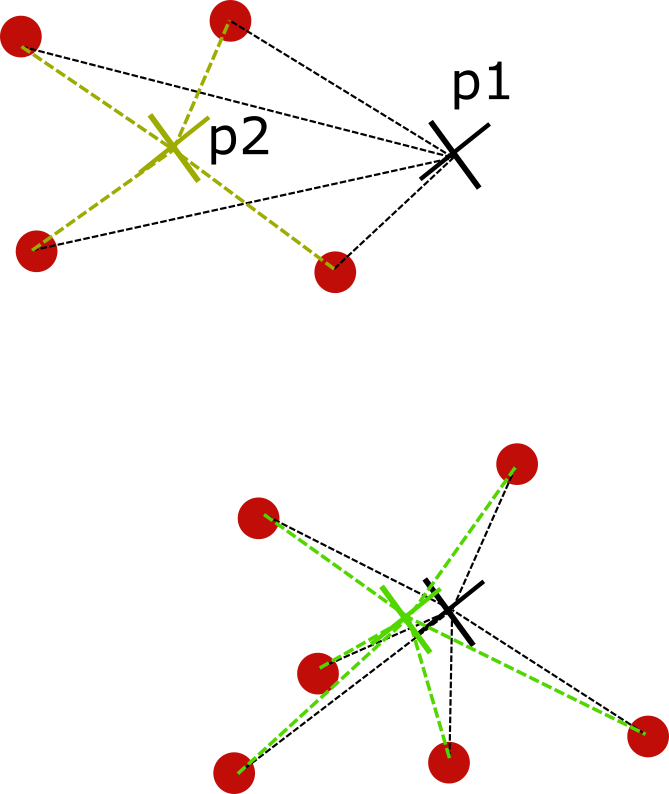
In the picture above, $p1$ represents the initial cluster position and $p2$ is center-of-mass. The algorithm continues until the change in the cluster positions is within a certain margin of error, indicating that it has converged.
The problem can be formulated as follows:
- Find cluster positions $c_1,c_2\ldots,c_N$ and labels $l$ such that we minimize
Here, $N_l$ is the number of data-points in cluster $l$. The algorithm depends strongly on the initial positions and it is not guaranteed that it will achieve a global optimum. Step 2 of the algorithm consists in atributing labels $l$ for the data-points $x$ such that $D$ is minimized given the centers of the clusters $c_l$. In step 3, we minimize with respect to the center positions $c_l$, that is,
\[\begin{equation}\begin{split} &\frac{\partial D}{\partial c_l}=\sum_{x\in \text{cluster: }l}(x_l-c_l)=0\\ &\Leftrightarrow c_l=\frac{1}{N_l}\sum_{x\in \text{cluster: }l} x_l \end{split}\end{equation}\]Statistical point of view
Consider the mixture gaussian model:
\[\begin{equation}\begin{split} &P(x|c)=\frac{1}{\sigma_c\sqrt{2\pi}}\exp{-\frac{(x-x_c)^2}{2\sigma_c^2}} \\ &P(c)=\frac{1}{N} \end{split}\end{equation}\]The probability $P(x)$ is
\[P(x)=\sum_c P(x|c)P(c)=\sum_c\frac{1}{N\sigma_c\sqrt{2\pi}}\exp{-\frac{|x-x_c|^2}{2\sigma_c^2}}\]We want to use maximum-likelihood estimation to determine the centers $x_c$. Therefore, we want to maximize the likelihood:
\[L=\sum_{x^i}\ln P(x^i)\]This is can be hard to solve because $P(x)$ contains a sum over multiple terms. However, we can approximate $P(x^i)$ by the cluster $c(i)$ that is closer to $x^i$, that is,
\[P(x^i)\simeq \frac{1}{N\sigma_c\sqrt{2\pi}}\exp{-\frac{|x^i-x_{c(i)}|^2}{2\sigma_c^2}}\]The approximation is valid provided there is a clear separation between the clusters, so the clusters different from $c(i)$ have exponentially suppressed contributions. That is, we need
\[\frac{|x^i-x_{c(i)}|^2}{\sigma_{c(i)}}\ll \frac{|x^i-x_{c'}|^2}{\sigma_{c'}},\;c(i)\neq c'\]then the likelihood function is:
\[L=\sum_{x^i}\ln P(x^i)\simeq -\frac{1}{2\sigma_{c(i)}^2}\sum_{x^i} |x^i-x_{c(i)}|^2\]Maximizing $L$ is equivalent to minimizing:
\[\sum_{x^i} \frac{1}{\sigma_{c(i)}^2}|x^i-x_{c(i)}|^2=\sum_{c} \frac{1}{\sigma_{c(i)}^2}\sum_{x\in \text{cluster}}|x^i-x_{c(i)}|^2\]Provided all the clusters have the same variance $\sigma_c=\sigma$, we recover the kmeans algorithm.
Python Implementation
The Python code is:
class Kmeans:
"""
KMeans algorithm:
* initialization: assigns random positions to clusters given mean
and standard deviation of data
"""
def __init__(self,n_clusters=5,epsilon=0.01):
self.n_clusters=n_clusters
self.epsilon=epsilon
# position centers for each iteration
self.centers_pos=[]
# centers positions: clusters_centers[i]=(x,y) for center i
self.clusters_centers=None
def fit(self,x):
std_dev=x.std(0)
#pick N random data-points
idx=np.random.choice(np.arange(x.shape[0]),self.n_clusters,replace=False)
#initialize center positions
self.clusters_centers=x[idx]+std_dev
self.clusters=[]
not_converged=True
while not_converged:
self.centers_pos.append(self.clusters_centers)
# calculate new
new_centers=self.newpos(x)
dev=new_centers-self.clusters_centers
self.clusters_centers=new_centers
dev=(dev*dev).sum(1)
dev=np.sqrt(dev)
if (dev>=self.epsilon).sum()==0:
not_converged=False
print('Converged')
#determine new means given clusters
def newpos(self,x):
distances=[]
for x_cl in self.clusters_centers:
d=x-x_cl
d=(d*d).sum(1)
d=np.sqrt(d)
distances.append(d.reshape(-1,1))
distances=np.concatenate(distances,axis=1)
self.clusters=distances.argmin(1)
#re-evaluate cluster centers
centers=self.clusters_centers.copy()
for i in range(self.n_clusters):
idx=(self.clusters==i)
if idx.sum()!=0:
new_center=x[idx].mean(0)
centers[i]=new_center
return centers
Then we generate data as:
N=4 #number of clusters
centers=np.random.normal(0,6,(N,2))
xs=[]
xcenters=np.zeros((100*N,2))
for c,i in zip(centers,range(5)):
a,b=c
x=c+np.random.normal(0,1,(100,2))
xcenters[i*100:100*(i+1),:]=c
xs.append(x)
xs_all=np.concatenate(xs)
that is,
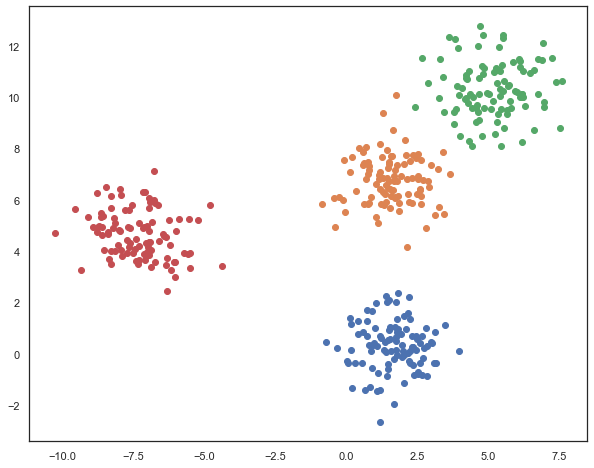
To solve the problem instantiate the object and run fit method:
km=Kmeans(N,0.01)
km.fit(xs_all)
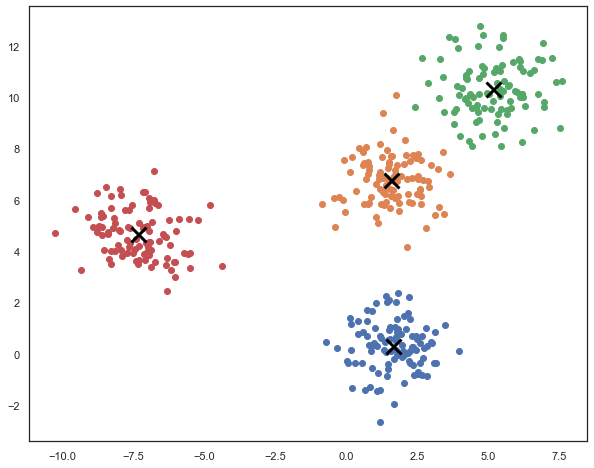
The dark crosses represent the solution of the k-means algorithm. We can keep track of the iterations:
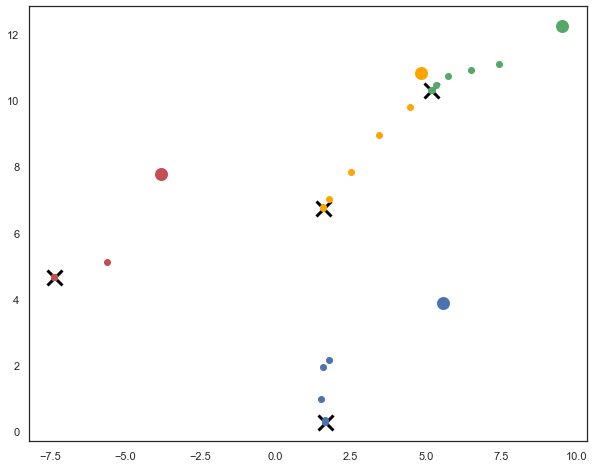
The larger circle represents the initial position, and subsequent smaller circles are the intermediate positions until convergence.