Statistical Testing
- Student’s t-test
- One-sample mean
- Two-sample mean
- Regression coefficient
- Correlation
- Chi square test
- Pearson’s Chi-square test
- Variance
1. Student’s t-test
- One-sample mean
Consider $n$ random variables distributed i.i.d., each following a normal distribution with mean $\mu$ and variance $\sigma$. The joint probability density function is
\[\frac{1}{(\sqrt{2\pi}\sigma)^n} e^{-\sum_{i=1}^{n}\frac{(x_i-\mu)^2}{2\sigma^2}}\prod_{i=1}^n dx_i\]We want to write a density distribution as a function of $\bar{x}=\frac{\sum_i x_i}{n}$, the sample mean. As such, use the equality
\[\sum_{i=1}^n(x_i-\mu)^2=\sum_{i=1}^n (x_i-\bar{x})^2+n(\bar{x}-\mu)^2\]and change variables $(x_1,\ldots,x_n)\rightarrow (x_1,\ldots,x_{n-1},\bar{x})$ - the jacobian of the coordinate transformation is $n$. The density function becomes
\[\frac{1}{(\sqrt{2\pi}\sigma)^n} e^{-\sum_{i=1}^{n}\frac{(x_i-\bar{x})^2}{2\sigma^2}-n\frac{(\bar{x}-\mu)^2}{2\sigma^2}}d\bar{x}\prod_{i=1}^{n-1} dx_i\]Because $x_i$ and $\bar{x}$ are independent, we can shift the variables $x_i\rightarrow x_i+\bar{x}$, after which the term $\sum_{i=1}^{n}(x_i-\bar{x})^2$ becomes $\sum_{i=1}^{n-1}x_i^2+(\sum_i^{n-1}x_i)^2$. Since this is quadratic in the $x_i$, it can be safely integrated out. However, before doing that we write
\[x_i=\frac{s}{\sqrt{n-1}}u_i\], with
\[\sum_{i=1}^{n-1}u_i^2+(\sum_i^{n-1}u_i)^2=1\], that is, $(s,u_i)$ play a similar role to spherical coordinates. The density distribution becomes
\[\frac{1}{(\sqrt{2\pi}\sigma)^n} e^{-(n-1)\frac{s^2}{2\sigma^2}-n\frac{(\bar{x}-\mu)^2}{2\sigma^2}}s^{n-2}\,\Omega(u_i)dsd\bar{x}\prod_{i=1}^{n-1} du_i\]where $\Omega(u_i)$ is a measure for the variables $u_i$- it gives an overall constant that we determine at the end instead.
To remove dependence on the variance $\sigma$ we consider the variable $t=(\bar{x}-\mu)\sqrt{n}/s$, which gives the Jacobian $s/\sqrt{n}$. We scale $s\rightarrow \sqrt{\frac{2}{n-1}}s\sigma$ to obtain
\[\propto \int_{s=0}^{\infty}e^{-s^2(1+\frac{1}{n-1}t^2)}s^{n-1}\,dsdt\]By changing $s\rightarrow \sqrt{s}$ we obtain
\[\propto\Big(1+\frac{1}{n-1}t^2\Big)^{-\frac{n}{2}}\Gamma(n/2)dt\]and integrating over $t: (-\infty,\infty)$ we fix the overall constant
\[\frac{\Gamma(n/2)}{\sqrt{(n-1)\pi}\Gamma(\frac{n-1}{2})}\Big (1+\frac{1}{n-1}t^2\Big)^{-\frac{n}{2}}\]This is known as the Student’s t-distribution with $\nu=n-1$ degrees of freedom.
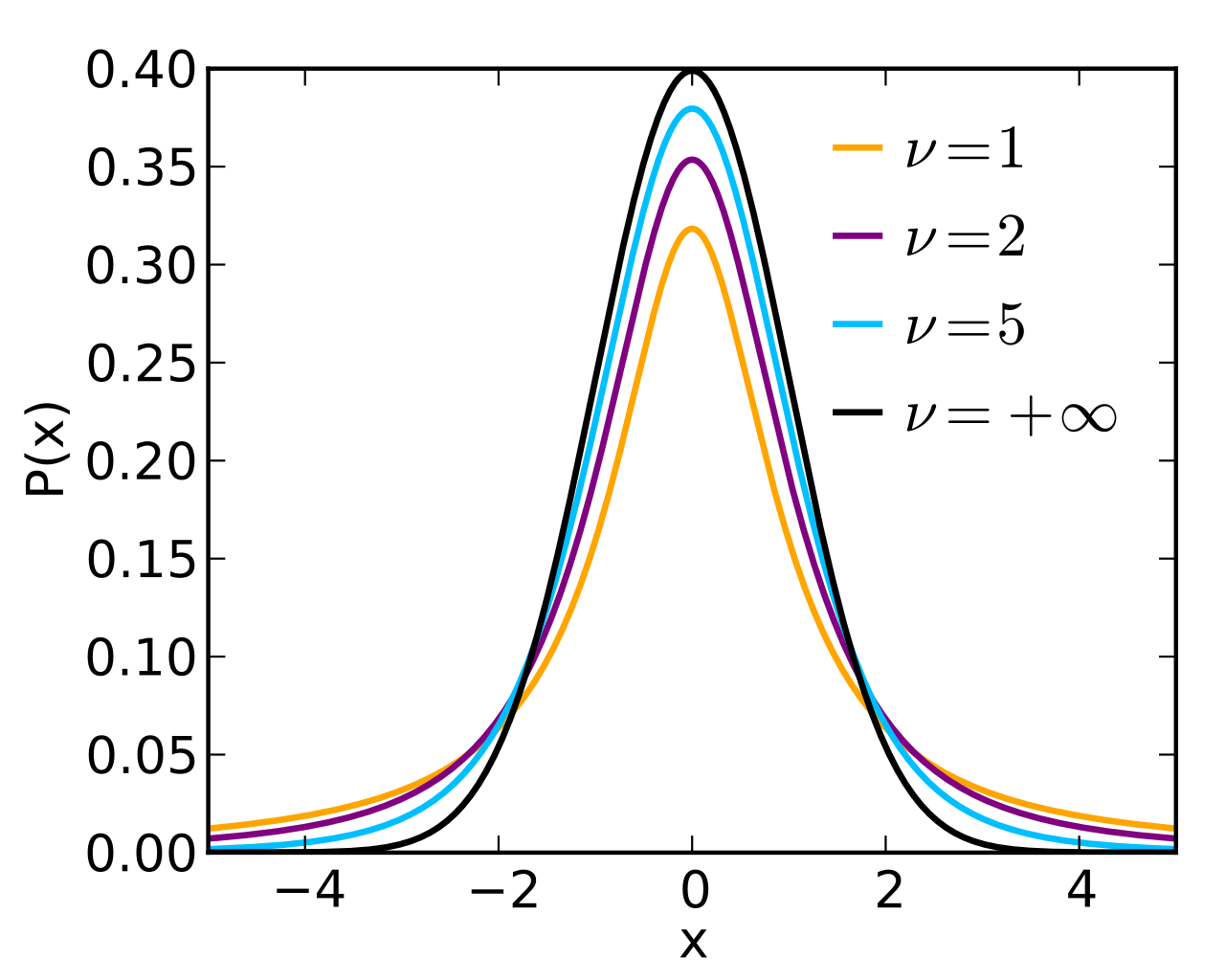
- Two-sample mean (equal variance)
For two samples with sizes $n_1,n_2$, the idea is roughly the same. We follow similar steps as in the previous case. After some algebra, the exponential contains the terms
\[-(n_1-1)\frac{s_1^2}{2\sigma^2}-(n_2-1)\frac{s_2^2}{2\sigma^2}-n_1\frac{(\bar{x}_1-\mu_1)^2}{2\sigma^2}-n_2\frac{(\bar{x}_2-\mu_2)^2}{2\sigma^2}\]where $s_1$ and $s_2$ are the two sample means.
Now we write \(\bar{x}_1-\mu_1=(\bar{x}_{+}+\bar{x}_{-})/2\) and \(\bar{x}_2-\mu_2=(\bar{x}_{+}-\bar{x}_{-})/2\), because we will want to integrate over \(\bar{x}_{+}\) . We use the equality
\[-n_1(\bar{x}_1-\mu_1)^2-n_2(\bar{x}_2-\mu_2)^2=-\frac{\bar{x}_{-}^2}{1/n_1+1/n_2}-\frac{n_1+n_2}{4}\Big(\bar{x}_{+}+\frac{n_1-n_2}{n_1+n_2}\bar{x}_{-}\Big)^2\]and integrate over $\bar{x}_{+}$. So we are left with
\[-(n_1-1)\frac{s_1^2}{2\sigma^2}-(n_2-1)\frac{s_2^2}{2\sigma^2}-\frac{\bar{x}_{-}^2}{(1/n_1+1/n_2)2\sigma^2}\]By writing
\[s^2=\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2},\;t=\frac{\bar{x}_{-}}{s\sqrt{1/n_1+1/n_2}}\]we obtain again the t-distribution with $\nu=n_1+n_2-2$ degrees of freedom.
- Regression coefficient
In linear regression, we assume that the target $y$ is a linear combination of the feature $x$ up to a gaussian noise, that is,
\[y=ax+b+\epsilon\]where $\epsilon$ is the noise distributed i.i.d according to a normal distribution with mean zero. Here $a,b$ are the true parameters that we want to estimate. In linear regression we use least square error to determine the estimators
\[\hat{a}=\frac{\sum_i(y_i-\bar{y})(x_i-\bar{x})}{\sum_i(x_i-\bar{x})^2},\;\hat{b}=\bar{y}-\hat{a}\bar{x}\]We want to calculate a probability for the difference $\hat{a}-a$. To do this we substitute $y_i=ax_i+b+\epsilon_i$ in the estimator equation. This gives
\[\hat{a}-a=\frac{\sum_i (\epsilon_i-\bar{\epsilon})(x_i-\bar{x})}{\sum_i(x_i-\bar{x})^2},\;\; \hat{b}-b=(a-\hat{a})\bar{x}+\bar{\epsilon}\]Since $\epsilon$ is normally distributed we want determine the probability of the quantity above. To facilitate the algebra we use vectorial notation. As such
\[\frac{\overrightarrow{\zeta}\cdot\overrightarrow{\gamma}}{\|\overrightarrow{\gamma}\|^2}\equiv\frac{\sum_i (\epsilon_i-\bar{\epsilon})(x_i-\bar{x})}{\sum_i(x_i-\bar{x})^2},\;\;\hat{b}-b=-\frac{\overrightarrow{\zeta}\cdot\overrightarrow{\gamma}}{\|\overrightarrow{\gamma}\|^2}\bar{x}+\overrightarrow{\epsilon}\cdot \overrightarrow{1}\]where $\overrightarrow{\gamma}\equiv x_i-\bar{x}$, $\zeta\equiv \epsilon_i-\bar{\epsilon}$ and $\overrightarrow{1}=(1,1,1,\ldots,1)/n$, a vector of ones divided by the number of datapoints. Note that
\[\overrightarrow{\gamma}\cdot \overrightarrow{1}=0,\;\;\overrightarrow{\zeta}\cdot \overrightarrow{1}=0\]The probability density function is proportional to the exponential of
\[-\frac{\|\overrightarrow{\epsilon}\|^2}{2\sigma^2}\]We write \(\overrightarrow{\epsilon}=\overrightarrow{\epsilon}_{\perp}+\alpha\overrightarrow{\gamma}+\beta\overrightarrow{1}\) with \(\overrightarrow{\epsilon}_{\perp}\cdot \overrightarrow{\gamma}=\overrightarrow{\epsilon}_{\perp}\cdot \overrightarrow{1}=0\). We calculate
\[\frac{\overrightarrow{\zeta}\cdot\overrightarrow{\gamma}}{\|\overrightarrow{\gamma}\|^2}=\alpha,\;\; \|\overrightarrow{\epsilon}\|^2=\|\overrightarrow{\epsilon}_{\perp}\|^2+\alpha^2\|\overrightarrow{\gamma}\|^2+\frac{\beta^2}{n}\]Integrating out $\beta$ we can build a t-test like variable with $n-2$ degrees of freedom, since $\overrightarrow{\epsilon}_{\perp}$ lives in a $n-2$ dimensional vector space. That is, \(t=\frac{\alpha\|\overrightarrow{\gamma}\|}{\|\overrightarrow{\epsilon}_{\perp}\|}\sqrt{n-2}\)
One can show that $|\overrightarrow{\epsilon}_{\perp}|^2=\sum_i(y_i-\hat{y}_i)^2$, and therefore
\[t=\frac{\hat{a}-a}{\sqrt{\frac{\sum_i(y_i-\hat{y}_i)^2}{\sum_i(x_i-\bar{x}_i)^2}}}\sqrt{n-2}\]For the intercept the logic is similar. We have
\[\hat{b}-b=-\frac{\overrightarrow{\zeta}\cdot\overrightarrow{\gamma}}{\|\overrightarrow{\gamma}\|^2}\bar{x}+\overrightarrow{\epsilon}\cdot \overrightarrow{1}=-\alpha\bar{x}+\frac{\beta}{n}\]and thus
\[\|\overrightarrow{\epsilon}\|^2=\|\overrightarrow{\epsilon}_{\perp}\|^2+\alpha^2\|\overrightarrow{\gamma}\|^2+n(\hat{b}-b+\alpha\bar{x})^2\]Integrating out $\alpha$ one finds that
\[t_{\text{intercept}}=\frac{(\hat{b}-b)\|\overrightarrow{\gamma}\|\sqrt{n-2}}{\|\overrightarrow{\epsilon}_{\perp}\|\sqrt{\|\overrightarrow{\gamma}\|^2/n+\bar{x}^2}}\]follows the Student’s t-distribution with $n-2$ degrees of freedom.
- Correlation
We want to test whether two variables $y$ and $x$ have zero correlation, statistically speaking. Essentialy this accounts to fit $y\sim ax+b$. We have seen that the regression coefficient $a$ is proportional to the sample correlation coefficient, that is,
\[a=\frac{\langle yx\rangle -\langle y\rangle \langle x\rangle}{\langle x^2\rangle -\langle x\rangle^2 }=r\frac{\sigma(y)}{\sigma(x)}\]where $\sigma(y)^2=\sum_{i}(y_i-\bar{y})^2/n$ and $\sigma(x)^2=\sum_{i}(x_i-\bar{x})^2/n$, and $r$ is the Pearson’s correlation coefficient. Then we use the equality
\[\sum_{i}(y_i-\hat{y}_i)^2/n=\sigma(y)^2(1-r^2)\]to find that the t-statistic for the regression coefficient $a$ can be written as
\[t=\frac{r\sqrt{n-2}}{\sqrt{1-r^2}}\]assuming that true coefficient is zero, that is, $a=0$.
2. Chi square test
Let each $X_i,\,i=1\ldots n$ be a random variable following a standard normal distribution. Then the sum of squares
\[\chi^2=\sum_{i=1}^nX^2_i\]follows a chi-distribution with $k$ degrees of freedom. To understand this, consider the joint probability density function of $n$ standard normal random variables
\[e^{-\frac{1}{2}\sum_{i=1}^n X_i^2}\prod_{i=1}^n dX_i\]If we use spherical coordinates with
\[X_i=ru_i,\;\sum_{i=1}^n u_i^2=1\]the probability density becomes
\[e^{-\frac{r^2}{2}}drr^{n-1}\Omega\]where $\Omega$ comes from integrating out $u_i$. Since $r$ is never negative we further use $s=r^{2}$ and obtain
\[\propto e^{-\frac{s}{2}}s^{\frac{n}{2}-1}ds\]Therefore the chi-square variable $\chi^2\equiv s$ with $k$ degrees of freedom follows the distribution
\[\chi^2\sim \frac{s^{\frac{n}{2}-1}}{2^{n/2}\Gamma(n/2)}e^{-\frac{s}{2}}\]This distribution has the following shape (from Wikipedia):

- Pearson’s Chi-square test
This test gives a measure of goodness of fit for a categorical variable with $k$ classes. Suppose we have $n$ observations with $x_i$ ($i=1\ldots k$) observed numbers, that is, $\sum_{i=1}^k x_i=n$. We want to test the hypotheses that each category is drawn with probability $p_i$. Under this assumption, the joint probability of observing $x_i$ numbers follows a multinomial distribution
\[P(x_1,x_2,\ldots,x_n)=\frac{n!}{x_1!x_2!\ldots x_k!}p_1^{x_1}p_2^{x_2}\ldots p_k^{x_k}\]We want to understand the behaviour of this probability when $n$ is very large. Assume that $x_i$ is also sufficiently large, which is ok to do for typical observations. In this case use stirling’s approximation of the factorial, that is,
\[n!\simeq \sqrt{2\pi n}\Big(\frac{n}{e}\Big)^n\]to write
\[P(x_1,x_2,\ldots,x_n)\propto \Big(\frac{n}{e}\Big)^n \prod_{i=1}^k \Big(\frac{x_i}{e}\Big)^{-x_i}p_i^{x_i}\]In taking $n$ very large, we want to keep the frequency $\lambda_i=x_i/ n$ fixed. Then the logarithm of the above expression becomes
\[\ln P(x_1,x_2,\ldots,x_n)=-\sum_{i=1}^k\lambda_in\ln(\lambda_i)+\sum_{i=1}^k\lambda_i n\ln(p_i)\]Since this is proportional to $n$ we can perform an asymptotic expansion as $n\gg 1$. We perform the expansion around the maximum of $\ln P$ (note that $\ln P$ is a concave function of $\lambda_i$ ), that is,
\[\frac{\partial P}{\partial \lambda_i}=0,\;i=1\ldots n-1\]Using the fact that we have $n-1$ independent variables since $\sum_i \lambda_i=1$, the solution is $\lambda_i^*=p_i$. Expanding around this solution we find
\[\ln P(\lambda_1,\lambda_2,\ldots,\lambda_n)=-n\sum_{i=1}^k\frac{(\lambda_i-p_i)^2}{2p_i}\]In terms of $x_i$ this gives
\[\ln P(x_1,x_2,\ldots,x_n)=-\sum_{i=1}^k\frac{(x_i-m_i)^2}{2m_i}\]where $m_i=np_i$ is the expected observed number. Therefore the quantity
\[\sum_{i=1}^k\frac{(x_i-m_i)^2}{m_i}\]follows a $\chi^2$ distribution with $k-1$ degrees of fredom, since only $k-1$ of the $x$’s are independent.
- Variance
In order to investigate the difference between the sample variance $s^2=\sum_i(x_i-\bar{x})^2/n-1$ and the assumed variance $\sigma^2$ of the distribution. We calculate \((n-1)\frac{s^2}{\sigma^2}\) Remember that for a normally distributed random variable $x_i$, the sum $\sum_i(x_i-\bar{x})^2$ also follows a normal distribution. In particular, the combination $\sum_i(x_i-\bar{x})^2/\sigma^2$ follows a $\chi^2$ distribution with $n-1$ degrees of freedom, because we have integrated out $\bar{x}$ as explained in the beginning of the post.