Statistical Power

The power statistic is defined as the probability

power=P(reject H0∣H1 True)\text{power}=P(\text{reject }H_0|H_1\text{ True})

where H0H_0 is the null hypothesis and H1H_1 is the alternative hypothesis.

We can model the t-statistics of both hypothesis using the Student’s t-distribution.

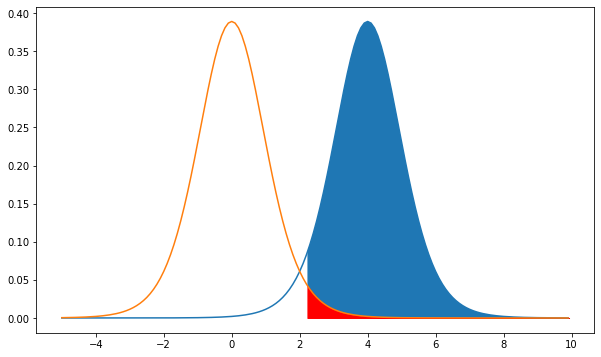
On the right is the distribution for the H1H_1 hypothesis while on the left we have the H0H_0 or null hypothesis. The area in red is the probability of rejecting the null hypothesis given that H0H_0 is true. This is the significance level that is usually is set to 5%. The area in blue is the probability of rejecting the null given that H1H_1 is true. If the distributions are far apart then the power approaches 1, while if they are close to each other the power is small.

Consider a statistical test for the difference of means of two samples with equal sizes n1=n2=nn_1=n_2=n and variance. The t-statistic is

t=Xˉ1−Xˉ2sp2nt=\frac{\bar{X}_1-\bar{X}_2}{s_p\sqrt{\frac{2}{n}}}

where sps_p is the pooled variance:

sp2=s12+s222s_p^2=\frac{s_1^2+s_2^2}{2}

and df=2n−2\text{df}=2n-2 are the number of degrees of freedom.

For large nn the Student t-distribution approaches a standard normal distribution. So we can calculate the power as

power=∫tα∞dte−(t−t∗)2/22π=1−Φ(tα−t∗)\text{power}=\int_{t_{\alpha}}^{\infty}dt\frac{e^{-(t-t^*)^2/2}}{\sqrt{2\pi}}=1-\Phi(t_{\alpha}-t^*)

Here tαt_{\alpha} is the value for which the null hypothesis is rejected, and t∗t^* is the expected value when H1H_1 is true.

The value of power is usually set at 80%, which means that Φ(tα−t∗)=0.2\Phi(t_{\alpha}-t^*)=0.2 or:

t∗−tα≃0.842t^*-t_{\alpha}\simeq 0.842

while tα≃1.96t_{\alpha}\simeq 1.96, which is the value for which Φ(tα)=0.975\Phi(t_{\alpha})=0.975. Definining the effect size as:

d=Xˉ1−Xˉ2spd=\frac{\bar{X}_1-\bar{X}_2}{s_p}

we can calculate the sample size with

n=2(1.96+0.842)2/d2n=2(1.96+0.842)^2/d^2