Hyperplanes and classification

1. Hyperplanes

Consider a set of $d+1$ points in $\mathbb{R}^{d}$ dimensions and assume that no group of three points is collinear- this way, any set of $d$ points forms a hyperplane. Firstly, we shall demonstrate that if a set of $d$ points is shattered in $\mathbb{R}^{d-1}$ dimensions, then $d+1$ points are also shattered in $\mathbb{R}^d$. We can use this to reduce the problem to two dimensions, where we have seen that $VC_{\text{dim}}=3$.

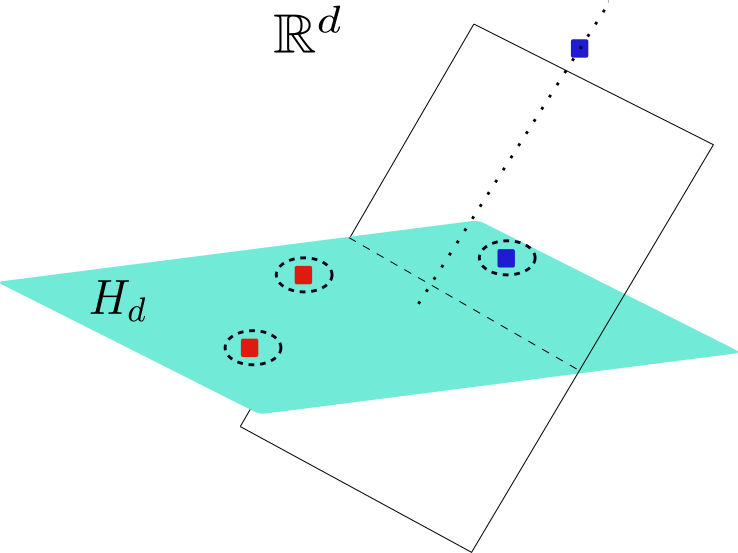
Consider the representation in the picture below. Choose $d$ points and take the hyperplane formed by these. If the remaining point belongs to the hyperplane, then we can consider the projection to $d-1$ dimensions, and we are left with the case of $(d-1)+2$ points in $\mathbb{R}^{d-1}$, which we shall analyze later. If this is not the case, then we can show that if the $d$ points on the hyperplane are separable, we can always find a hyperplane in $\mathbb{R}^d$ that separates all the points. In the figure below, the dashed line on $H_d$ represents the hyperplane in $\mathbb{R}^{d-1}$ that separates the set of $d$ points. It is easy to see that any hyperplane that contains the remaining point and the dashed line (hyperplane in one lower dimension) is the solution to this problem.

We shall consider now the case of $d+2$ points in $\mathbb{R}^d$. For this purpose, we shall use Radon’s theorem that states that any set of $d+2$ points in $\mathbb{R}^d$ can be partitioned in two sets $X_1$ and $X_2$ such that the corresponding convex hulls intersect. This theorem implies that $d+2$ points in $\mathbb{R}^d$ cannot be shattered because if they were, then we would have two non-intersecting convex hulls separated by a plane, thus contradicting the theorem.

Proof

For $d+2$ points $x_i$ in $\mathbb{R}^d$ one can always choose $d+2$ parameters $\alpha_i$ such that:

$$\sum_{i=1}^{d+2}\alpha_ix_i=0,\;\; \sum_{i=1}^{d+2}\alpha_i=0$$

The reason is because one has $d+2$ unknowns ($\alpha_i$) for $d+1$ equations ($d$ coming from the first vector equation and an additional from the constraint on $\alpha$). The second equation can be rewritten as a sum over positive $\alpha_{>}$ and negative $\alpha_{<}$, that is, $\sum_{i}\alpha_i^{>}=\sum_{i}\alpha_i^{<}$. Define $\alpha=\sum_i\alpha_i^{>}$, then we have

$$\sum_i\frac{\alpha_i^{>}}{\alpha}=\sum_i\frac{\alpha_i^{<}}{\alpha}$$

which is a sum over numbers in the interval $(0,1]$. The vector equation separates into two terms

$$\sum_{i}\frac{\alpha_i^{>}}{\alpha}x_i=\sum_i\frac{\alpha_i^{<}}{\alpha}x_i$$

and each of the sets $X_1={x_i: \alpha_i^{>}\neq 0}$ and $X_2={x_i: \alpha_i^{<}\neq 0}$ form convex hulls. This means that $X_1$ and $X_2$ intersect.

References

[1] Foundations of machine learning, M. Mohri, A. Rostamizadeh, A. Talwalkar