Decision Tree
1. The algorithm
The decision tree algorithm consists of a sequence of splits, or decisions, which take the form of a tree. This tree organizes the data in a way that there is a gain of information at each node.
A measure of information is the Shannon entropy, defined as
\[S=-\sum_i p_i\ln(p_i)\]with \(p_i\) the probability of the element $i$ in a set $\Omega$. The Shannon entropy is always smaller than the most entropic configuration which happens for \(p_i=1/|\Omega|\) , with $|\Omega|$ the number of elements in the set. To see this, write $p_i=n_i/|\Omega|$ where $n_i$ is the number of elements in class $i$. Therefore
\[-\sum_ip_i\ln(p_i)=-\sum_ip_i\ln\Big(\frac{n_i}{|\Omega|}\Big)<\ln|\Omega|\]This means that more diverse the set is, larger the entropy.
At each node in the decision tree, a feature $f_i$ and a threshold $t_i$ is chosen so that the entropy of the left split $f_i< t_i$ plus the entropy of the right split $f_i\geq t_i$ is smaller than the entropy of the initial configuration $A$. That is,
\[S(A)> S(A_{f_i< t_i})+S(A_{f_i\geq t_i})\]In the example below we have 7 balls: 3 of color red, 2 green, 1 pink and 1 blue.

We want to determine a rule that predicts the ball’s color as a function of $x$. For that purpose, we build a decision tree containing splits with thresholds as a function of $x$.

Following, we show that this particular tree provides information gains at each step of the splits. The entropy of the initial configuration is
\[S=-\frac{3}{7}\ln\big(\frac{3}{7}\big)-\frac{2}{7}\ln\big(\frac{2}{7}\big)-\frac{2}{7}\ln\big(\frac{1}{7}\big)\simeq 1.277\]After the first split the entropy on the left and right sides of the node is reduced to $0$ and $1.034$ respectively. Their sum is smaller than the initial entropy $1.277$. The next split at $x=b$ results in two configurations with entropies $0$ on the left and $0.69$ on the right side of the split. The last split classifies unequivocally the configuration resulting in splits with zero entropy.
The decision tree algorithm consists of the following steps:
\[\begin{equation*}\begin{split} \text{for i}&=1\ldots \text{Depth}:\\ & \text{for j}=1\ldots \text{Leaves}:\\ & \;\;\text{Choose feature and threshold }(f,t)=\text{argmin}_{f,t} S(A_{f< t})+S(A_{f\geq t}) \end{split}\end{equation*}\]That is, at each depth level we loop through each of the leaves and split if there is gain in information. Then we continue one step further in depth. The predictor consists in attributing the majority class at each ending node.
In the case of regression, each split consists in chosing a feature $f$ and threshold $t$ so that the sum of the mean squared errors of the left and right split configurations is minimized. That is
\[\text{Split }(f,t)=\text{argmin}_{f,t} \sum_{i\in A_l}(y_i-\bar{y}_l)^2+\sum_{i\in A_r}(y_i-\bar{y}_r)^2\]where $A_l,A_r$ are the left and right split configurations, and $\bar{y}_l,\bar{y}_r$ are the average values in each of the configurations.
Other measures of information gain
The Gini index, defined as
\[G=1-\sum_ip_i^2\]provides another measure of information. The gini index is a bounded quantity that is $0\leq G<1$, unlike the Shannon entropy. Noting that $\sum_i p_i=1$ we can write $G=\sum_i p_i(1-p_i)$. For $p_i=1-\epsilon$ with $\epsilon\ll 1$ we can approximate $-p_i\ln p_i\simeq \epsilon(1-\epsilon)=p_i(1-p_i)$. Analogously for $p_i\simeq \epsilon$ we can approximate
\[p_i(1-p_i)\simeq -(1-p_i)\ln(1-p_i)\]Therefore for distributions which are concentrated in a particular class the gini index is an approximation to the Shannon entropy. One of the advantages of using the Gini index is its simpler computational complexity due to its polynomial form compared to the logarithm in the Shannon entropy.
Time complexity
Take a note as an example. A practical algorithm for the split consists of sorting the data for each of the features and then choosing the threshold that produces higher information gains. Calculating the frequencies for each threshold is of order $\mathcal{O}(N)$, with $N$ the number of samples. Therefore, finding the right split is of order $\mathcal{O}(dN\log N)$, with $d$ the number of features. The number of splits increases exponentially with the depth, but the number of samples per node decreases exponentially, which gives a net effect of $\mathcal{O}(dN\log N)$ at each depth. Since the maximum depth attainable is of order $\log N$, the total time complexity of training a decision tree should be at most $\mathcal{O}(dN\log^2 N)$
Sample complexity
Consider a binary classification problem where the feature space is of the form $\chi={0,1}^d$, with $d$ the dimension. It is easy to see that a tree with depth $d$ has $2^d$ leaves and can represent all data points in $\chi$. The $\text{VC}$-dimension is therefore $\text{VC}_{dim}=2^d$.
2. Decision Boundary
Below we depict the sucession of splits for a 2-dimensional feature space. As we can see the tree divides the feature space into successive rectangles.
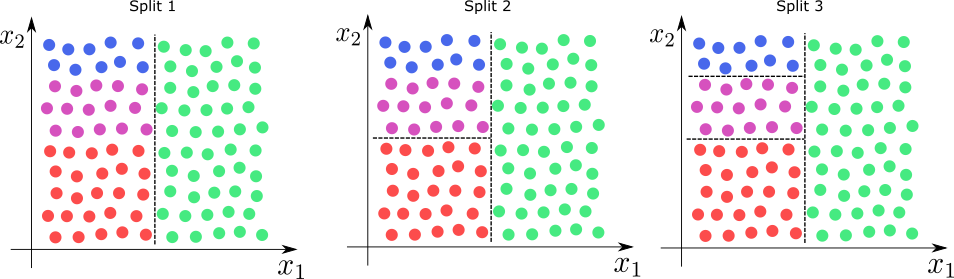
For large depth the tree can lead to highly non-linear decision bondaries.
3. Python implementation
First we create a Binary-Search-Tree data structure. This tree is composed of a main node, and pointers to a left and right nodes, which are generated during the split. The main node contains a subset of the data, the corresponding Shannon-entropy, the depth of the node, the selected feature and threshold, and the predicted class.
class Node:
def __init__(self,cl_dic,entropy=None,feature=None,idx=None,depth=None):
self.feature=feature # (feature_num, threshold)
self.idx_subset=idx
self.depth=depth
self.entropy=entropy
self.cl_dic=cl_dic
self.right=None
self.left=None
self.prediction=None
#method cross_entropy determines the Shannon-entropy of the subset at the main node
def cross_entropy(self,y,idx):
subset=y[idx]
z=np.zeros(len(self.cl_dic))
for t in subset:
k=self.cl_dic[t]
z[k]+=1
pred=z.argmax()
z=z/z.sum()
z=np.where(z==0,1,z)
ent=-z*np.log2(z)
ent=ent.sum()
return pred,ent
#the entropy_split method takes in an array of frequencies and returns the best split that leads to the highest gains in information
def entropy_split(self,freq):
z=freq.copy()
w=freq.copy()
w=w/w.sum(1).reshape(-1,1)
w=np.where(w==0,1,w)
entropy1=-w*np.log2(w)
entropy1=entropy1.sum(1)
z=z[-1]-z
s=z.sum(1).reshape(-1,1)
s[-1][0]=1
z=z/s
z=np.where(z==0,1,z)
entropy2=-z*np.log2(z)
entropy2=entropy2.sum(1)
total=entropy1+entropy2
j=total.argmin()
return j,entropy1[j],entropy2[j]
#the method best_feature loops through all the features and chooses the best split
def best_feature(self,x,y,idx_subset):
w=np.zeros(x.shape[1])
indices=[]
pos=[]
for f in range(x.shape[1]):
idx=np.argsort(x[:,f],axis=0)
indices.append(idx.copy())
y_sort=y[idx]
z=np.zeros((x.shape[0],len(self.cl_dic)))
cum=np.zeros(z.shape[1])
for i,t in enumerate(y_sort):
k=self.cl_dic[t]
cum[k]+=1
z[i]=cum[:]
j,e1,e2=self.entropy_split(z)
pos.append(j)
w[f]=e1+e2
num=w.argmin() #best feature index
idx=indices[num]
j=pos[num]
value=x[idx][j,num]
#multiple values for the same feature
i=0
while x[idx][j+i,num]==value:
i+=1
j=j+i-1
value=x[idx][j:j+2,num].mean()
idx_left=idx_subset[idx[:j+1]]
idx_right=idx_subset[idx[j+1:]]
pred_l,entropy_left=self.cross_entropy(y,idx[:j+1])
pred_r,entropy_right=self.cross_entropy(y,idx[j+1:])
j=pos[num]
return num,value,pred_l,entropy_left,pred_r,entropy_right,idx_left,idx_right
# the split method runs through all the nodes in the tree and splits them
def split(self,node,x,y):
if node is not None and node.entropy==0:
pass
if node is not None and node.feature is None:
#split
idx=node.idx_subset
a,b,pl,el,pr,er,idl,idr=self.best_feature(x[idx],y[idx],idx)
node.feature=(a,b)
node.right=Node(entropy=er,idx=idr,depth=node.depth+1,cl_dic=node.cl_dic)
node.right.prediction=pr #prediction
node.left=Node(entropy=el,idx=idl,depth=node.depth+1,cl_dic=node.cl_dic)
node.left.prediction=pl #prediction
elif node is not None and node.feature is not None:
#go down on tree
self.split(node.right,x,y)
self.split(node.left,x,y)
The Decision Tree classifier is build upon the Node class with a fit and a predict methods.
class DTreeClassifier:
def __init__(self,criterion='entropy',depth=None):
self.criterion='entropy'
print('Using entropy criterion')
self.max_depth=depth
self.classes=None
self.num_features=None
self.head=None
def fit(self,x,y):
self.classes=sorted(list(set(y)))
self.num_features=x.shape[1]
cl_dic={c:i for i,c in enumerate(self.classes)}
idx=np.arange(x.shape[0])
self.head=Node(cl_dic=cl_dic,idx=idx,depth=0)
_,self.head.entropy=self.head.cross_entropy(y,idx)
for i in range(self.max_depth):
self.head.split(self.head,x,y)
#private method
def __recurrence(self,node,x):
if node is not None and node.feature is not None:
f,threshold=node.feature
if x[f]>threshold:
return self.__recurrence(node.right,x)
else:
return self.__recurrence(node.left,x)
elif node is not None and node.feature is None:
return node.prediction
def predict(self,x):
pred=np.zeros(x.shape[0])
for i,xi in enumerate(x):
pred[i]=self.__recurrence(self.head,xi)
return pred