Cross Validation
Fold Generation
To build a machine learning model, we usually separate the dataset into training and validation sets. The training dataset is used for learning and the validation set for hyperparameter tuning. If enough data is available, we might consider a test set that we use to estimate the error. This is the desired approach. However, it requires considerable data for training, validation, and testing.
When the dataset is small, it may not be appropriate to separate the data into three sets because this can result in insufficient data for training. In cross-validation, the dataset $D$ is separated into $n$ mutually-exclusive sets or folds $F_i$
\[D=\cup_{i=1}^n F_i,\qquad F_i\cap F_j=\emptyset,\,i\neq j\]For each fold, we train the model in the complement dataset $D\setminus F_i$ and perform validation in $F_i$. For each fold, we calculate a metric, resulting in $n$ sample estimates. Compare with the usual approach for which only one sample estimate is calculated. This is very useful because now we can see how the metric estimate spreads. If there is much of variation, the model is likely overfitting. Despite training with a small dataset that can lead to overfitting, cross-validation compensates this by providing several error estimates.
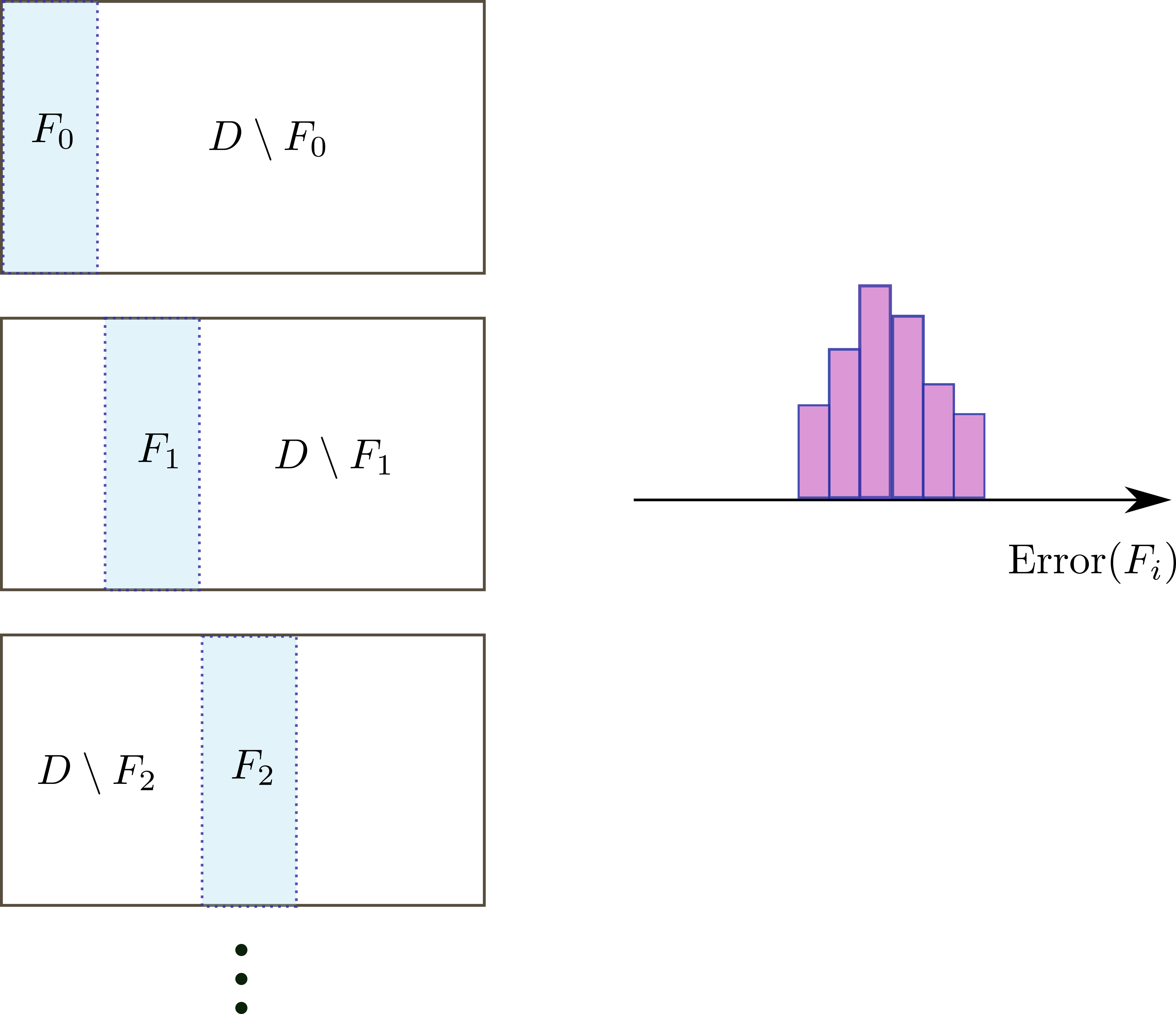
K-Fold
In K-fold cross validation we split the dataset in a set of mutually exclusive $K$ folds. First we shuffle the dataset, to remove any bias related to ordering.
import pandas as pd
import numpy as np
from sklearn.ensemble import RandomForestRegressor
from sklearn.datasets import load_boston
data=load_boston()
df=pd.DataFrame(data['data'],columns=data['feature_names'])
df['target']=data['target']
class KFold:
def __init__(self,cv) -> None:
self.cv=cv
def folds(self,data):
df=data.sample(frac=1)
n=df.shape[0]//self.cv
idx=np.zeros(df.shape[0]).astype('bool')
for f in range(self.cv):
if f==self.cv-1:
idx[f*n:]=True
else:
idx[f*n:(f+1)*n]=True
yield df[~idx],df[idx]
idx[f*n:(f+1)*n]=False
cv=KFold(10)
gen=cv.folds(df)
scores=[]
for dftrain, dval in gen:
rf=RandomForestRegressor(10)
x=dftrain.drop(columns='target')
y=dftrain['target']
rf.fit(x,y)
xval=dval.drop(columns='target')
yval=dval['target']
sc=rf.score(xval,yval)
scores.append(sc)
#In this case we calculate the R^2, coefficient of determination
print(scores)
[0.8012382297305908,
0.8045356517296745,
0.9128662279013549,
0.8846474088861058,
0.7757146590797888,
0.8857988005069696,
0.8908495305590521,
0.6937581845597063,
0.8771969286141039,
0.8699437438827288]
scores=np.array(scores)
print(scores.mean())
0.8396549365450076
print(scores.std())
0.06522622191732715
What if we consider more folds?
cv=KFold(20)
print(scores.mean())
0.8303582842929952
print(scores.std())
0.12374214944566267
The average score is approximately the same but the standard deviation has increased two-fold. For a large number of folds, it is expected the variation to increase and the model to perform worse.
means=[]
stds=[]
ns=np.arange(5,101,5)
for n in ns:
cv=KFold(n)
gen=cv.folds(df)
scores=[]
for dftrain, dval in gen:
rf=RandomForestRegressor(10)
x=dftrain.drop(columns='target')
y=dftrain['target']
rf.fit(x,y)
xval=dval.drop(columns='target')
yval=dval['target']
sc=rf.score(xval,yval)
scores.append(sc)
scores=np.array(scores)
m=scores.mean()
std=scores.std()
means.append(m)
stds.append(std)
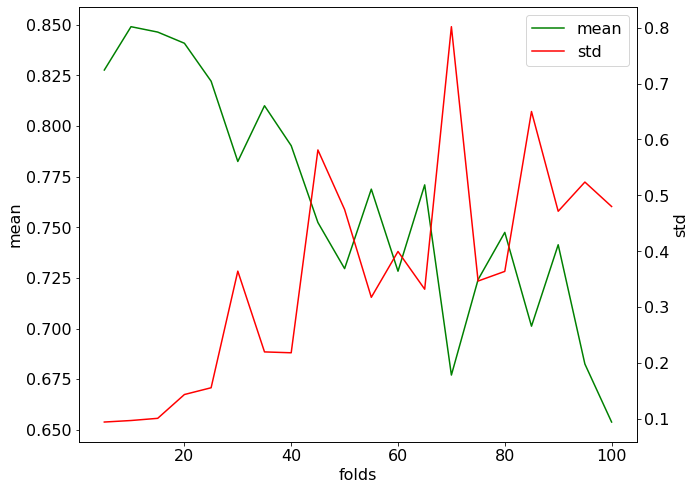
We see the model’s performance deteriorating with an increasing number of folds. This is because the training folds have an increasing number of datapoints in common, favoring overfitting. At the same time, the folds become smaller, which increases the variance of the error. We see in the above plot that the standard deviation is increasing.
Stratified
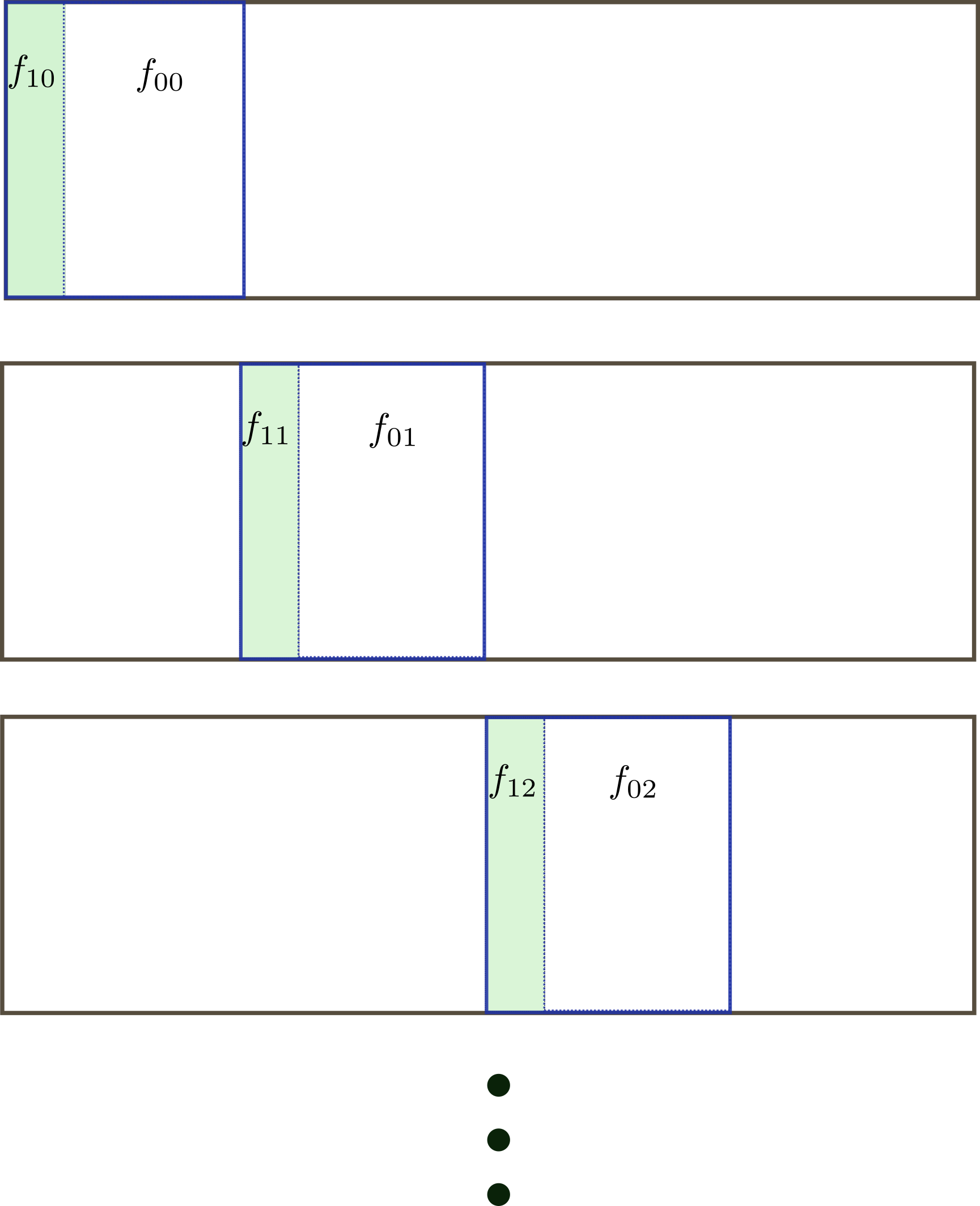
In stratified cross-validation, each fold preserves the proportions between classes. If the dataset is unbalanced, a fold in K-fold cross validation can miss an entire class. First we create folds $f_{1i}$, with labels $y=1$, and $f_{0i}$ with labels $y=0$.

Each fold $F_i$ is built by joining the sets $f_{1i}$ with $f_{0i}$:
class KStratified:
def __init__(self,cv) -> None:
self.cv=cv
def folds(self,data):
df=data.sample(frac=1)
idx_1 = data['target']==1
cv=KFold(self.cv)
df1=df[idx_1]
df0=df[~idx_1]
for f1, f0 in zip(cv.folds(df1),cv.folds(df0)):
f1a,f1b=f1
f0a,f0b=f0
dfa=pd.concat([f1a,f0a],axis=0)
dfb=pd.concat([f1b,f0b],axis=0)
yield dfa, dfb