-
May 2, 2020
The Rademacher complexity measures how a hypothesis correlates with noise. This gives a way to evaluate the capacity or complexity of a hypothesis class.
-
May 1, 2020
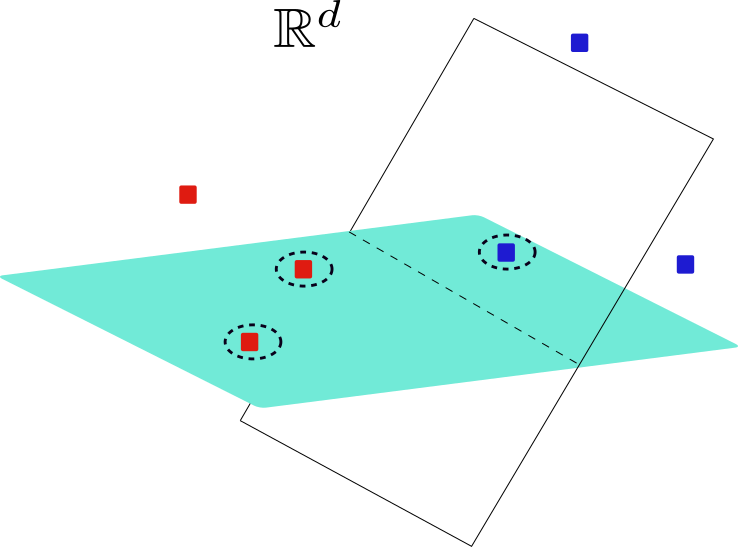
We study binary classification problem in R**d using hyperplanes. We show that the VC dimension is d+1.
-
Apr 30, 2020
The VC dimension is a fundamental concept in machine learning theory. It gives a measure of complexity based on combinatorial aspects. This concept is used to show how certain infinite hypothesis classes are PAC-learnable. Some of the main ideas are explained: growth function and shattering. I give examples and show how the VC dimension can bound the generalization error.
-
Apr 26, 2020
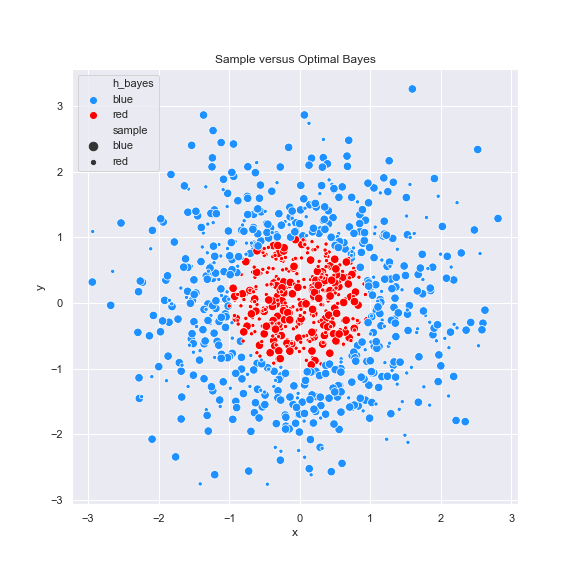
The Bayes optimal classifier achieves minimal error across all possible classifiers. We give a proof of this and provide some numerical examples.
-
Apr 14, 2020
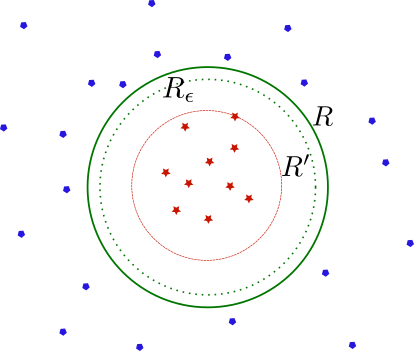
In this post I explain some of the fundamentals of machine learning: PAC learnability, overfitting and generalisation bounds for classification problems. I show how these concepts work in detail for the problem of learning circumferences.